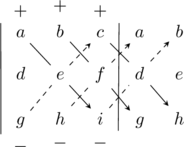Outil de calcul du déterminant d'une matrice. Le déterminant d'une matrice carré M est une valeur calculées à partir des éléments la composant noté det(M) ou encore |M|.
Déterminant d'une Matrice - dCode
Catégorie(s) : Matrice
dCode est gratuit et ses outils sont une aide précieuse dans les jeux, les maths, les énigmes, les géocaches, et les problèmes à résoudre au quotidien !
Une suggestion ? un problème ? une idée ? Écrire à dCode !
Déterminant d'une Matrice
Calcul de Déterminant d'une Matrice 2x2
Calcul de Déterminant d'une Matrice 3x3
Calcul de Déterminant d'une Matrice 4x4
Calcul de Déterminant d'une Matrice NxN
Réponses aux Questions (FAQ)
Qu'est-ce que le déterminant d'une matrice ? (Définition)
Le déterminant d'une matrice est une valeur associée à une matrice (ou aux vecteur la définissant), cette valeur est très pratique dans divers calculs matriciels.
Comment calculer le déterminant d'une matrice ?
Pour une matrice carrée d'ordre 2 (2x2), effectuer le calcul :
$$ \begin{vmatrix} a & b \\ c & d \end{vmatrix} = ad - bc $$
Un moyen mnémotechnique est de soustraire la première diagonale à la seconde.
Exemple : $$ \begin{vmatrix} 1 & 2 \\ 3 & 4 \end{vmatrix} = 1 \times 4 - 2 \times 3 = -2 $$
Pour les matrices de taille supérieure comme 3x3, le déterminant d'ordre 3 se calcule :
$$ \begin{vmatrix} a & b & c \\ d & e & f \\ g & h & i \end{vmatrix} = a \begin{vmatrix} e & f \\ h & i \end{vmatrix} - b \begin{vmatrix} d & f \\ g & i \end{vmatrix} + c \begin{vmatrix} d & e \\ g & h \end{vmatrix} \\ = aei-afh+bfg-bdi+cdh-ceg $$
Les sous-matrices calculées sont appelées des mineurs de la matrice originale.
L'idée est la même pour les matrices d'ordre supérieur :
Pour une matrice 4x4, le déterminant d'ordre 4 est:
$$ \begin{vmatrix} a & b & c & d \\ e & f & g & h \\ i & j & k & l \\ m & n & o & p \end{vmatrix} = a \begin{vmatrix} f & g & h \\ j & k & l \\ n & o & p \end{vmatrix} - b \begin{vmatrix} e & g & h \\ i & k & l \\ m & o & p \end{vmatrix} + c \begin{vmatrix} e & f & h \\ i & j & l \\ m & n & p \end{vmatrix} - d \begin{vmatrix} e & f & g \\ i & j & k \\ m & n & o \end{vmatrix} \\ = \\ a(fkp − flo − gjp + gln + hjo − hkn) − b(ekp − elo − gip + glm + hio − hkm) + c(ejp − eln − fip + flm + hin − hjm) − d(ejo − ekn − fio + fkm + gin − gjm) \\ = \\ afkp − aflo − agjp + agln + ahjo − ahkn − bekp + belo + bgip − bglm − bhio + bhkm + cejp − celn − cfip + cflm + chin − chjm − dejo + dekn + dfio − dfkm − dgin + dgjm $$
Comment calculer le déterminant d'une matrice non carré ?
Le déterminant d'une matrice non carrée n'est pas défini, il n'existe pas selon la définition du déterminant.
Quelle est la formule de calcul de déterminant d'une matrice d'ordre n ?
Il n'existe pas de formule autre que l'explication ci-dessus pour le cas général d'une matrice d'ordre n.
Comment calculer le déterminant d'une matrice 1x1 ?
Pour une matrice 1x1, le déterminant est le seul élément de la matrice.
Exemple : $$ | 1 | = 1 $$
Quel est le déterminant d'une matrice identité ?
Une matrice identité a pour déterminant $ 1 $.
Exemple : $$ \begin{vmatrix} 1 & 0 \\ 0 & 1 \end{vmatrix} = 1 \times 1 - 0 \times 0 $$
Exemple : $$ \begin{vmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{vmatrix} = ( 1 \times 1 \times 1) - (1 \times 0 \times 0) + (0 \times 0 \times 0) - (0 \times 0 \times 1) + (0 \times 0 \times 0) - (0 \times 1 \times 0) = 1 $$
Seul le terme correspond à la multiplication de la diagonale vaudra 1 et les autres termes seront nuls.
Quel est le déterminant d'une matrice transposée ?
Une matrice transposée a le même déterminant que la matrice non transposée et donc une matrice a le même déterminant que sa propre matrice transposée.
Comment trouver le déterminant d'une matrice à partir de ses valeurs propres ?
Le déterminant d'une matrice $ M $ est le produit de ses valeurs propres (valeurs complexes et éventuelle multiplicité comprises).
Cette propriété est valable pour toute taille de matrice carrée (2x2, 3x3, 4x4, 5x5, etc.)
Code source
dCode se réserve la propriété du code source pour "Déterminant d'une Matrice". Sauf code licence open source explicite (indiqué Creative Commons / gratuit), l'algorithme pour "Déterminant d'une Matrice", l'applet ou snippet (convertisseur, solveur, chiffrement / déchiffrement, encodage / décodage, encryptage / décryptage, traducteur) ou les fonctions liées à "Déterminant d'une Matrice" (calculer, convertir, résoudre, décrypter / encrypter, déchiffrer / chiffrer, décoder / encoder, traduire) codés en langage informatique (Python, Java, C#, PHP, Javascript, Matlab, etc.) ou les données, en téléchargement, script, ou les accès API à "Déterminant d'une Matrice" ne sont pas publics, idem pour un usage hors ligne, PC, mobile, tablette, appli iPhone ou Android !
Rappel : dCode est gratuit.
Citation
Le copier-coller de la page "Déterminant d'une Matrice" ou de ses résultats est autorisée (même pour un usage commercial) tant que vous créditez dCode !
L'exportation des résultats sous forme de fichier .csv ou .txt est gratuite en cliquant sur l'icone export
Citer comme source bibliographique :
Déterminant d'une Matrice sur dCode.fr [site web en ligne], consulté le 19/12/2024,
- Calcul de Déterminant d'une Matrice 2x2
- Calcul de Déterminant d'une Matrice 3x3
- Calcul de Déterminant d'une Matrice 4x4
- Calcul de Déterminant d'une Matrice NxN
- Qu'est-ce que le déterminant d'une matrice ? (Définition)
- Comment calculer le déterminant d'une matrice ?
- Comment calculer le déterminant d'une matrice non carré ?
- Quelle est la formule de calcul de déterminant d'une matrice d'ordre n ?
- Comment calculer le déterminant d'une matrice 1x1 ?
- Quel est le déterminant d'une matrice identité ?
- Quel est le déterminant d'une matrice transposée ?
- Comment trouver le déterminant d'une matrice à partir de ses valeurs propres ?
