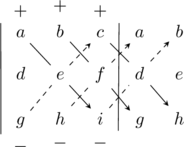Tool to compute a matrix determinant. The determinant of a square matrix M is a useful value computed from its inner elements and denoted det(M) or |M|.
Determinant of a Matrix - dCode
Tag(s) : Matrix
dCode is free and its tools are a valuable help in games, maths, geocaching, puzzles and problems to solve every day!
A suggestion ? a feedback ? a bug ? an idea ? Write to dCode!
Determinant of a Matrix
Matrix 2x2 Determinant Calculator
Matrix 3x3 Determinant Calculator
Matrix 4x4 Determinant Calculator
Matrix NxN Determinant Calculator
Answers to Questions (FAQ)
What is the matrix determinant? (Definition)
The determinant of a matrix is a value associated with a matrix (or the vectors defining it), noted $ \det(M) $ or $ |M| $, this value is calculated from the coefficients of the matrix and is used in various matrix calculations.
How to calculate a matrix determinant?
For a 2x2 square matrix (order 2), the calculation is:
$$ \begin{vmatrix} a & b \\ c & d \end{vmatrix} = ad - bc $$
Example: $$ \begin{vmatrix} 1 & 2 \\ 3 & 4 \end{vmatrix} = 1 \times 4 - 2 \times 3 = -2 $$
For higher size matrix like order 3 (3x3), compute:
$$ \begin{vmatrix} a & b & c \\ d & e & f \\ g & h & i \end{vmatrix} = a \begin{vmatrix} e & f \\ h & i \end{vmatrix} - b \begin{vmatrix} d & f \\ g & i \end{vmatrix} + c \begin{vmatrix} d & e \\ g & h \end{vmatrix} \\ = aei-afh+bfg-bdi+cdh-ceg $$
The calculated sub-matrices are called minors of the original matrix.
The idea is the same for higher matrix sizes:
For an order 4 determinant of a 4x4 matrix:
$$ \begin{vmatrix} a & b & c & d \\ e & f & g & h \\ i & j & k & l \\ m & n & o & p \end{vmatrix} = a \begin{vmatrix} f & g & h \\ j & k & l \\ n & o & p \end{vmatrix} - b \begin{vmatrix} e & g & h \\ i & k & l \\ m & o & p \end{vmatrix} + c \begin{vmatrix} e & f & h \\ i & j & l \\ m & n & p \end{vmatrix} - d \begin{vmatrix} e & f & g \\ i & j & k \\ m & n & o \end{vmatrix} \\ = \\ a(fkp − flo − gjp + gln + hjo − hkn) − b(ekp − elo − gip + glm + hio − hkm) + c(ejp − eln − fip + flm + hin − hjm) − d(ejo − ekn − fio + fkm + gin − gjm) \\ = \\ afkp − aflo − agjp + agln + ahjo − ahkn − bekp + belo + bgip − bglm − bhio + bhkm + cejp − celn − cfip + cflm + chin − chjm − dejo + dekn + dfio − dfkm − dgin + dgjm $$
dCode offers an online determinant calculator that can calculate the determinant for any matrix size. By default dCode considers $ i $ as the imaginary unit of complex numbers.
What is the formula for calculating the determinant of a matrix of order n?
There is no other formula than the explanation above for the general case of a matrix of order n.
How to compute the determinant of a matrix 1x1?
For a 1x1 matrix, the determinant is the only item of the matrix.
Example: $$ | 1 | = 1 $$
What is the determinant of an identity matrix?
An identity matrix $ I_n $ has for determinant $ 1 $ whatever the value of $ n $.
Example: $$ \begin{vmatrix} 1 & 0 \\ 0 & 1 \end{vmatrix} = 1 \times 1 - 0 \times 0 $$
Example: $$ \begin{vmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{vmatrix} = ( 1 \times 1 \times 1) - (1 \times 0 \times 0) + (0 \times 0 \times 0) - (0 \times 0 \times 1) + (0 \times 0 \times 0) - (0 \times 1 \times 0) = 1 $$
Only the term corresponding to the multiplication of the diagonal will be 1 and the other terms will be null.
What is the Rule of Sarrus?
The Sarrus Rule is a practical method for manually calculating the determinant of a 3×3 matrix quickly by copying 2 columns:
The determinant of M is calculated as follows $ (aei+bfg+cdh) - (gec+hfa-idb) $, it is a subtraction of 2 sums. The first is composed of the multiplication of the elements of the three main diagonals (from top to bottom, from left to right) $ aei $, $ bfg $ and $ cdh $ and the second of the multiplication of the elements of the three secondary diagonals (from bottom to top, from left to right) $ gec $, $ hfa $ and $ idb $
How to calculate the determinant for a non square matrix?
The determinant of a non-square matrix is not defined, it does not exist according to the definition of the determinant.
What is the determinant of a transpose matrix?
A transpose matrix has the same determinant as the untransposed matrix and hence a matrix has the same determinant as its own transpose matrix.
How to find a matrix determinant from its eigenvalues?
The determinant of a matrix is the product of its eigenvalues (including complex values and potential multiplicity).
This property is valid for any size of square matrix (2x2, 3x3, 4x4, 5x5, etc.)
How do you know if a matrix is invertible with its determinant?
A matrix M is invertible if and only if its determinant is non-zero.
If $ \det(M) \neq 0 $, then $ M $ is invertible.
How to quickly calculate the determinant when the matrix has identical rows (or columns)?
If two rows (or columns) of a matrix are identical, then its determinant is zero (= 0).
Source code
dCode retains ownership of the "Determinant of a Matrix" source code. Any algorithm for the "Determinant of a Matrix" algorithm, applet or snippet or script (converter, solver, encryption / decryption, encoding / decoding, ciphering / deciphering, breaker, translator), or any "Determinant of a Matrix" functions (calculate, convert, solve, decrypt / encrypt, decipher / cipher, decode / encode, translate) written in any informatic language (Python, Java, PHP, C#, Javascript, Matlab, etc.) or any database download or API access for "Determinant of a Matrix" or any other element are not public (except explicit open source licence). Same with the download for offline use on PC, mobile, tablet, iPhone or Android app.
Reminder: dCode is an educational and teaching resource, accessible online for free and for everyone.
Cite dCode
The content of the page "Determinant of a Matrix" and its results may be freely copied and reused, including for commercial purposes, provided that dCode.fr is cited as the source (Creative Commons CC-BY free distribution license).
Exporting the results is free and can be done simply by clicking on the export icons ⤓ (.csv or .txt format) or ⧉ (copy and paste).
To cite dCode.fr on another website, use the link:
In a scientific article or book, the recommended bibliographic citation is: Determinant of a Matrix on dCode.fr [online website], retrieved on 2026-01-22,
- Matrix 2x2 Determinant Calculator
- Matrix 3x3 Determinant Calculator
- Matrix 4x4 Determinant Calculator
- Matrix NxN Determinant Calculator
- What is the matrix determinant? (Definition)
- How to calculate a matrix determinant?
- What is the formula for calculating the determinant of a matrix of order n?
- How to compute the determinant of a matrix 1x1?
- What is the determinant of an identity matrix?
- What is the Rule of Sarrus?
- How to calculate the determinant for a non square matrix?
- What is the determinant of a transpose matrix?
- How to find a matrix determinant from its eigenvalues?
- How do you know if a matrix is invertible with its determinant?
- How to quickly calculate the determinant when the matrix has identical rows (or columns)?