Logarithme

La définition du logarithme naturel est la fonction dont la dérivée est la fonction inverse de $ x \mapsto \frac 1 x $ définie pour $ x \in \mathbb{R}_+^* $.

Le logarithme naturel se note log ou ln et a pour base le nombre $ e \approx 2.71828\ldots $ (voir les décimales du nombre e).

Un logarithme en base $ N $ se calcule à partir de logarithme népériens selon la formule : $$ \log_{N}(x) = \frac {\ln(x)} {\ln(N)} $$

Il en découle que $ log_{a}(b) = \frac {\ln(b)} {\ln(a)} $ et $ log_{b}(a) = \frac {\ln(a)} {\ln(b)} $ sont des inverses

Le logarithme népérien est l'autre nom du logarithme naturel (donc en base e).

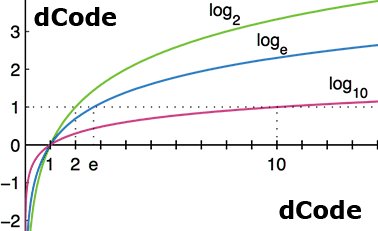
Le logarithme décimal noté $ \log_{10} $ ou log10 est le logarithme en base $ 10 $. C'est un des logarithmes les plus utilisé dans les calculs et les échelles logarithmiques. $$ \log_{10}(x) = \frac {\ln(x)} {\ln(10)} $$

Le logarithme binaire noté $ \log_{2} $ (ou parfois $ lb $) est le logarithme en base $ 2 $. C'est le logarithme utilisé principalement pour les calculs informatiques. $$ \log_2(x) = \frac {\ln(x)} {\ln(2)} $$

Tout logarithme a comme propriétés :

— $ \log_b(x \cdot y) = \log_b(x) +\log_b(y) $ (transformation d'un produit en somme)

— $ \log_b \left( \frac{x}{y} \right) = \log_b(x) - \log_b(y) $ (transformation d'un quotient en soustraction)

— $ \log_b (x^a) = a \log_b(x) $ (transformation d'une puissance en multiplication)

— $ \log_b(b) = 1 $

— $ \log(e) = \ln(e) = 1 $

— $ \log_{10}(10) = 1 $

— $ \log_b(1) = ln(1) = 0 $

— $ \log_b(b^n) = \ln(e^n) = n $ (fonction inverse de l'exponentiation)