Outil pour calculer la période d'une fonction : la valeur t telle que la fonction se répète f(x+t)=f(x-t)=f(x), ce qui est le cas des fonctions trigo (cos, sin, etc.).
Période d'une Fonction - dCode
Catégorie(s) : Fonctions
dCode est gratuit et ses outils sont une aide précieuse dans les jeux, les maths, les énigmes, les géocaches, et les problèmes à résoudre au quotidien !
Une suggestion ? un problème ? une idée ? Écrire à dCode !
Période d'une Fonction
Calculatrice de Période t
Réponses aux Questions (FAQ)
Qu'est ce qu'une période de fonction ? (Définition)
La période $ t $ d'une fonction périodique $ f(x) $ est la plus petite valeur $ t $ telle que $$ f(x+t) = f(x) $$
Graphiquement, sa courbe se reproduit sur l'intervalle de chaque période. La fonction est égale à elle-même chaque cycle de longueur $ t $ (elle présente un motif/graphe qui se répète par translation).
La valeur de la période $ t $ est aussi appelée périodicité d'une fonction ou période fondamentale.
Comment déterminer la période d'une fonction ?
Pour trouver la période $ t $ d'un signal ou d'une fonction périodique $ f(x) $, montrer que $$ f(x+t)=f(x) $$
Exemple : La fonction trigonométrique $ \sin(x + 2\pi) = \sin(x) $ donc $ \sin(x) $ est périodique de période $ 2\pi $ 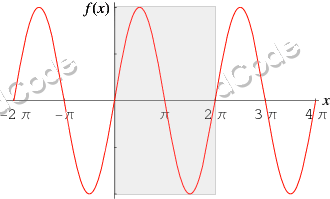
Les fonctions trigonométriques/sinusoidales sont généralement périodiques de période $ 2\pi $, pour deviner la valeur de $ t $, envisager des multiples de pi pour la valeur $ t $.
Si la période est nulle (égale à $ 0 $), alors la fonction n'est pas périodique.
Comment déterminer la valeur f(x) d'une fonction périodique ?
Toute fonction périodique de période $ t $ se répète toutes les $ t $ valeurs. Pour prédire la valeur du cycle d'une fonction périodique, pour une valeur $ x $ calculer $ x_t = x \mod t $ (modulo t) et rechercher la valeur connue de $ f(x_t) = f(x) $
Exemple : La fonction $ f(x) = \cos(x) $ a une période de $ 2\pi $, la valeur pour $ x = 9 \pi $ est la même que pour $ x \equiv 9 \pi \mod 2 \pi \equiv \pi \mod 2 \pi $ et donc $ \cos(9 \pi) = \cos(\pi) = -1 $
Comment déterminer l'amplitude d'une fonction ?
L'amplitude correspond à la valeur absolue de la partie non périodique de la fonction.
Exemple : $ a \sin(x) $ a pour amplitude $ | a | $
Comment prouver la périodicité d'une fonction ?
La démonstration de l'existence d'une période $ t $ pour une fonction $ f $ consiste à calculer si l'équation $ f(x+t)=f(x) $ est vraie.
Comment prouver qu'une fonction n'est pas périodique ?
Si $ f $ est périodique alors il existe un réel non nul tel que $$ f(x+t)=f(x) $$
La démonstration consiste à montrer que c'est impossible. Par exemple via un raisonnement par l'absurde ou en réalisant un calcul qui débouche sur une contradiction.
Quelles sont les fonctions périodiques usuelles ?
Les fonctions périodiques les plus courantes sont les fonctions trigonométriques à base de fonctions sinus et cosinus (qui ont une période de 2 Pi).
| Période de Sinus $ \sin(x) $ | $ 2\pi $ |
| Période de Cosinus $ \cos(x) $ | $ 2\pi $ |
| Période de Tangente $ \tan(x) $ | $ \pi $ |
Code source
dCode se réserve la propriété du code source pour "Période d'une Fonction". Tout algorithme pour "Période d'une Fonction", applet ou snippet ou script (convertisseur, solveur, chiffrement / déchiffrement, encodage / décodage, encryptage / décryptage, traducteur) ou toutes fonctions liées à "Période d'une Fonction" (calculer, convertir, résoudre, décrypter / encrypter, déchiffrer / chiffrer, décoder / encoder, traduire) codés en langage informatique (Python, Java, C#, PHP, Javascript, Matlab, etc.) ou toute base de données, ou accès API à "Période d'une Fonction" ou tout autre élément ne sont pas publics (sauf licence open source explicite). Idem avec le téléchargement pour un usage hors ligne sur PC, mobile, tablette, appli iPhone ou Android.
Rappel : dCode est une ressource éducative et pédagogique, accessible en ligne gratuitement et pour tous.
Citation
Le contenu de la page "Période d'une Fonction" ainsi que ses résultats peuvent être copiés et réutilisés librement, y compris à des fins commerciales, à condition de mentionner dCode.fr comme source (Licence de libre diffusion Creative Commons CC-BY).
L'export des résultats est gratuit et se fait simplement en cliquant sur les icônes d'export ⤓ (format .csv ou .txt) ou ⧉ copier-coller.
Pour citer dCode.fr sur un autre site Internet, utiliser le lien :
Dans un article scientifique ou un livre, la citation bibliographique recommandée est : Période d'une Fonction sur dCode.fr [site web en ligne], consulté le 27/02/2026,
- Calculatrice de Période t
- Qu'est ce qu'une période de fonction ? (Définition)
- Comment déterminer la période d'une fonction ?
- Comment déterminer la valeur f(x) d'une fonction périodique ?
- Comment déterminer l'amplitude d'une fonction ?
- Comment prouver la périodicité d'une fonction ?
- Comment prouver qu'une fonction n'est pas périodique ?
- Quelles sont les fonctions périodiques usuelles ?
