Outil pour générer des permutations d'éléments, soit les arrangements d'objets distincts selon tous les ordres : 123,132,213,231,312,321.
Permutations - dCode
Catégorie(s) : Combinatoire
dCode est gratuit et ses outils sont une aide précieuse dans les jeux, les maths, les énigmes, les géocaches, et les problèmes à résoudre au quotidien !
Une suggestion ? un problème ? une idée ? Écrire à dCode !
Permutations
Générateur de Permutations
Dénombrement de Permutations/Anagrammes
Réponses aux Questions (FAQ)
Qu'est ce qu'une permutation ? (Définition)
En mathématiques, les permutations d'éléments sont la liste de tous les arrangements (et ordonnancement) de ces éléments dans tous les ordres possibles.
Exemple : Les trois lettres A,B,C peuvent être mélangées (anagrammes) de 6 façons : A,B,C B,A,C C,A,B A,C,B B,C,A C,B,A
Les permutations ne doivent pas être confondues avec les combinaisons (pour lesquelles l'ordre n'a pas d'influence) ou avec les arrangements aussi appelées permutations partielles (permutations d'une partie des éléments).
Comment générer des permutations ?
La méthode la plus connue est l'algorithme de Heap (méthode utilisée par le calculateur de dCode).
Voici un pseudo code source : function permute(data, n) {
if (n = 1) print data
else {
for (i = 0 .. n-2) {
permute(data, n-1)
if (n % 2) swap(data[0], data[n-1])
else swap(data[i], data[n-1])
permute(data, n-1)
}
}
}
Les permutations peuvent ainsi être représentées sous forme d'un arbre des permutations : 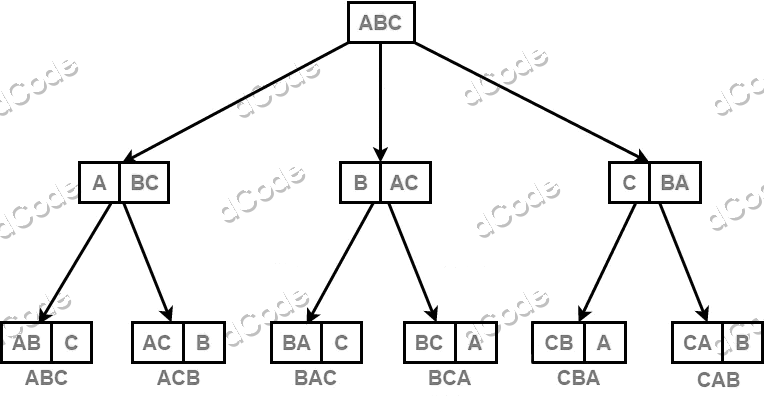
Un autre algorithme, nommé Johnson–Trotter génére toutes les permutations en ne modifiant qu'une paire d'éléments adjacents à chaque étape.
Comment compter les permutations ?
Le dénombrement du nombre total de permutations de $ n $ éléments distincts est donné par la factorielle : $$ n! = n \times (n−1) \times (n−2) \times \cdots \times 2 \times 1 $$
Exemple : Pour $ 4 $ éléments, le nombre de combinaisons est $ 4! = 24 $
Comment compter les permutations distinctes ?
Lorsqu'un ensemble contient des éléments répétés, certaines permutations sont identiques. Le nombre de permutations distinctes est alors donné par la formule : $$ \frac{ n! } { n_1! \times n_2! \times \cdots \times n_i! } $$ avec $ n_i $ le nombre d'occurrence de chaque élément répété.
Autrement dit, le fait d'avoir un élément qui se répète divise le nombre total de permutation par le nombre de permutations possibles pour les éléments répétés.
Exemple : Les 5 lettres de DCODE ont $ 5! = 120 $ permutations mais comprennent la lettre D en double (ces $ 2 $ lettres D ont $ 2! $ permutations), diviser le nombre total de permutations $ 5! $ par $ 2! $ soit $ 5!/2!=60 $ permutations distinctes.
Code source
dCode se réserve la propriété du code source pour "Permutations". Tout algorithme pour "Permutations", applet ou snippet ou script (convertisseur, solveur, chiffrement / déchiffrement, encodage / décodage, encryptage / décryptage, traducteur) ou toutes fonctions liées à "Permutations" (calculer, convertir, résoudre, décrypter / encrypter, déchiffrer / chiffrer, décoder / encoder, traduire) codés en langage informatique (Python, Java, C#, PHP, Javascript, Matlab, etc.) ou toute base de données, ou accès API à "Permutations" ou tout autre élément ne sont pas publics (sauf licence open source explicite). Idem avec le téléchargement pour un usage hors ligne sur PC, mobile, tablette, appli iPhone ou Android.
Rappel : dCode est une ressource éducative et pédagogique, accessible en ligne gratuitement et pour tous.
Citation
Le contenu de la page "Permutations" ainsi que ses résultats peuvent être copiés et réutilisés librement, y compris à des fins commerciales, à condition de mentionner dCode.fr comme source (Licence de libre diffusion Creative Commons CC-BY).
L'export des résultats est gratuit et se fait simplement en cliquant sur les icônes d'export ⤓ (format .csv ou .txt) ou ⧉ copier-coller.
Pour citer dCode.fr sur un autre site Internet, utiliser le lien :
Dans un article scientifique ou un livre, la citation bibliographique recommandée est : Permutations sur dCode.fr [site web en ligne], consulté le 13/02/2026,
