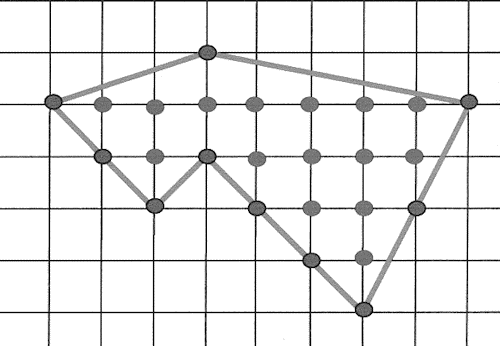
Outil pour appliquer et calculer une surface à l'aide du Théorème de Pick qui permet le calcul de l'aire d'un polygone positionné sur une grille orthogonale normée et dont les sommets sont des points de la grille.
Théorème de Pick - dCode
Catégorie(s) : Géométrie
dCode est gratuit et ses outils sont une aide précieuse dans les jeux, les maths, les énigmes, les géocaches, et les problèmes à résoudre au quotidien !
Une suggestion ? un problème ? une idée ? Écrire à dCode !
Théorème de Pick
Calculatrice selon Pick
Réponses aux Questions (FAQ)
Qu'est ce que le Théorème de Pick ? (Définition)
Le Théorème de Pick est une formule mathématique qui permet de calculer l'aire (surface) d'un polygone dont les sommets ont des coordonnées entières dans un plan cartésien (un quadrillage/grille 2D).
Pour un polygone à $ b $ sommets construit sur un quadrillage (les sommets sont des points de la grille) présentant $ i $ points à l'intérieur, la formule de Pick indique que l'aire $ A $ du polygone vaut $$ A = i + \frac{b}{2} - 1 $$
Tous les points présents sur le contour sont considérés comme des sommets (les angles des sommets sont plats dans ce cas).
Comment calculer une aire selon le Théorème de Pick ?
La formule de Pick demande deux paramètres : le nombre $ i $ de points intérieurs du polygone et le nombre $ b $ de points sur le contour/périmètre du polygone. L'aire $ A $ du polygone vaut $ A = i + \frac{b}{2} - 1 $
Exemple : Le polygone dessiné ci après 
possède 15 points à l'intérieur du polygone (gris clair), et 10 sommets (gris foncé). Son aire est donc de $ A = 15 + 10/2 - 1 = 19 $.
Le Théorème de Pick fonctionne-t-il pour les polygones concaves ?
Oui, le Théorème de Pick peut être appliqué à des polygones concaves tant que les sommets ont des coordonnées entières.
Comment utiliser le Théorème de Pick pour des polygones avec des trous à l'intérieur ?
Le Théorème de Pick ne s'applique qu'aux polygones simples sans trous à l'intérieur. Cependant, si le ou les trous forment un polygone éligible au Théorème de Pick, alors il est possible de calculer l'aire du polygone à trou (en ignorant les trous) et d'y soustraire les aires des trous pour obtenir l'aire du polygone avec des trous.
Qui a créé le Théorème de Pick ?
La formule doit son nom à Georg Alexander Pick qui l'a décrite en 1899.
Code source
dCode se réserve la propriété du code source pour "Théorème de Pick". Tout algorithme pour "Théorème de Pick", applet ou snippet ou script (convertisseur, solveur, chiffrement / déchiffrement, encodage / décodage, encryptage / décryptage, traducteur) ou toutes fonctions liées à "Théorème de Pick" (calculer, convertir, résoudre, décrypter / encrypter, déchiffrer / chiffrer, décoder / encoder, traduire) codés en langage informatique (Python, Java, C#, PHP, Javascript, Matlab, etc.) ou toute base de données, ou accès API à "Théorème de Pick" ou tout autre élément ne sont pas publics (sauf licence open source explicite). Idem avec le téléchargement pour un usage hors ligne sur PC, mobile, tablette, appli iPhone ou Android.
Rappel : dCode est une ressource éducative et pédagogique, accessible en ligne gratuitement et pour tous.
Citation
Le contenu de la page "Théorème de Pick" ainsi que ses résultats peuvent être copiés et réutilisés librement, y compris à des fins commerciales, à condition de mentionner dCode.fr comme source (Licence de libre diffusion Creative Commons CC-BY).
L'export des résultats est gratuit et se fait simplement en cliquant sur les icônes d'export ⤓ (format .csv ou .txt) ou ⧉ copier-coller.
Pour citer dCode.fr sur un autre site Internet, utiliser le lien :
Dans un article scientifique ou un livre, la citation bibliographique recommandée est : Théorème de Pick sur dCode.fr [site web en ligne], consulté le 12/07/2025,
- Calculatrice selon Pick
- Qu'est ce que le Théorème de Pick ? (Définition)
- Comment calculer une aire selon le Théorème de Pick ?
- Le Théorème de Pick fonctionne-t-il pour les polygones concaves ?
- Comment utiliser le Théorème de Pick pour des polygones avec des trous à l'intérieur ?
- Qui a créé le Théorème de Pick ?
