Tool to compute the period of a function: the value t such that the function repeats itself: f(x+t)=f(x-t)=f(x), that is the case for trigo functions (cos, sin, etc.)
Period of a Function - dCode
Tag(s) : Functions
dCode is free and its tools are a valuable help in games, maths, geocaching, puzzles and problems to solve every day!
A suggestion ? a feedback ? a bug ? an idea ? Write to dCode!
Period of a Function
Period of a Function Calculator
Answers to Questions (FAQ)
What is the period of a function? (Definition)
The period $ t $ of a periodic function $ f(x) $ is the smallest value $ t $ such that $$ f(x+t) = f(x) $$
Graphically, its curve is repeated over the interval of each period. The function is equal to itself for every cycle of length $ t $ (it presents a pattern/graph that is repeated by translation).
The value of the period $ t $ is also called the periodicity of the function or fundamental period.
How to find the period of a function?
To find the period $ t $ of a signal or a function $ f(x) $, demonstrate that $$ f(x+t)=f(x) $$
Example: The trigonometric function $ \sin(x + 2\pi) = \sin(x) $ so $ \sin(x) $ is periodic of period $ 2\pi $ 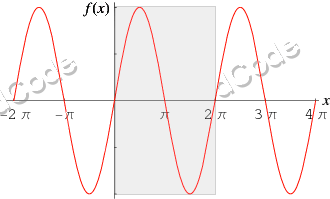
Trigonometric/sinusoidal functions are usually periodic, with a period $ 2\pi $, to guess the period, try multiples of pi for value $ t $.
If the period is equal to 0, then the function is not periodic.
How to find the value f(x) of a periodic function?
Any periodic function of period $ t $ repeats every $ t $ values. To predict the cycle value of a periodic function, for a value $ x $ calculate $ x_t = x \mod t $ (modulo t) and find the known value of $ f(x_t) = f(x) $
Example: The function $ f(x) = \cos(x) $ has a period of $ 2\pi $, the value for $ x = 9 \pi $ is the same as for $ x \equiv 9 \pi \mod 2 \pi \equiv \pi \mod 2 \pi $ and therefore $ \cos(9 \pi) = \cos(\pi) = -1 $
How to find the amplitude of a periodic function?
The amplitude is the absolute value of the non-periodic part of the function.
Example: $ a \sin(x) $ has for amplitude $ | a | $
How to prove the periodicity of a function?
The demonstration of the existence of a period $ t $ for a function $ f $ consists in calculating if the equation $ f(x+t)=f(x) $ is true.
How to prove that a function is not periodic?
If $ f $ is periodic, then it exists a real not null such as $$ f(x+t)=f(x) $$
Demonstration consists in proving that it is impossible. For example with a reductio ad absurdum or performing a calculation that leads to a contradiction.
What are usual periodic functions?
The most common periodic functions are trigonometric functions based on sine and cosine functions (which have a period of 2 Pi).
| Function | Period |
|---|---|
| Sine $ \sin(x) $ | $ 2\pi $ |
| Cosine $ \cos(x) $ | $ 2\pi $ |
| Tangent $ \tan(x) $ | $ \pi $ |
Source code
dCode retains ownership of the "Period of a Function" source code. Any algorithm for the "Period of a Function" algorithm, applet or snippet or script (converter, solver, encryption / decryption, encoding / decoding, ciphering / deciphering, breaker, translator), or any "Period of a Function" functions (calculate, convert, solve, decrypt / encrypt, decipher / cipher, decode / encode, translate) written in any informatic language (Python, Java, PHP, C#, Javascript, Matlab, etc.) or any database download or API access for "Period of a Function" or any other element are not public (except explicit open source licence). Same with the download for offline use on PC, mobile, tablet, iPhone or Android app.
Reminder: dCode is an educational and teaching resource, accessible online for free and for everyone.
Cite dCode
The content of the page "Period of a Function" and its results may be freely copied and reused, including for commercial purposes, provided that dCode.fr is cited as the source (Creative Commons CC-BY free distribution license).
Exporting the results is free and can be done simply by clicking on the export icons ⤓ (.csv or .txt format) or ⧉ (copy and paste).
To cite dCode.fr on another website, use the link:
In a scientific article or book, the recommended bibliographic citation is: Period of a Function on dCode.fr [online website], retrieved on 2025-11-17,
- Period of a Function Calculator
- What is the period of a function? (Definition)
- How to find the period of a function?
- How to find the value f(x) of a periodic function?
- How to find the amplitude of a periodic function?
- How to prove the periodicity of a function?
- How to prove that a function is not periodic?
- What are usual periodic functions?
