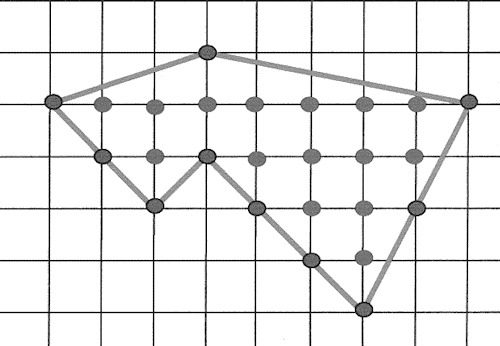
Tool to apply and calculate a surface using the Pick's Theorem that allows the calculation of the area of a polygon positioned on a lattice (normalized orthogonal grid) and whose vertices are points of the grid.
Pick's Theorem - dCode
Tag(s) : Geometry
dCode is free and its tools are a valuable help in games, maths, geocaching, puzzles and problems to solve every day!
A suggestion ? a feedback ? a bug ? an idea ? Write to dCode!
Pick's Theorem
Pick Polygon Area Calculator
Answers to Questions (FAQ)
What is the Pick Theorem? (Definition)
Pick's Theorem is a mathematical formula that allows you to calculate the area of a polygon whose vertices have integer coordinates in a Cartesian plane (a 2D grid/grid).
For a polygon with $ b $ vertices constructed on a grid (the vertices are grid points) having $ i $ points inside it, Pick's formula indicates that the area $ A $ of the polygon is $$ A = i + \frac{b}{2} - 1 $$
All points present on the contour are considered vertices (vertex angles are flat in this case).
How to calculate an area with the Pick Theorem?
Pick's formula requires two parameters: the number $ i $ of interior points of the polygon and the number $ b $ of points on the contour/perimeter of the polygon. The area $ A $ of the polygon is $ A = i + \frac{b}{2} - 1 $
Example: The polygon drawn below 
has 15 points inside the polygon (light gray), and 10 vertices (dark gray). Its area is therefore $ A = 15 + 10/2 - 1 = 19 $.
Does Pick's Theorem work for concave polygons?
Yes, Pick's Theorem can be applied to concave polygons as long as the vertices have integer coordinates.
How to use Pick's Theorem for polygons with holes inside?
Pick's Theorem only applies to simple polygons with no holes inside. However, if the hole(s) form a polygon eligible for Pick's Theorem, then it is possible to calculate the area of the hole polygon (ignoring the holes) and subtract the areas of the holes to obtain the area of the hole. polygon with holes.
Who created Pick's Theorem?
The formula owes its name to Georg Alexander Pick who described it in 1899.
Source code
dCode retains ownership of the "Pick's Theorem" source code. Except explicit open source licence (indicated Creative Commons / free), the "Pick's Theorem" algorithm, the applet or snippet (converter, solver, encryption / decryption, encoding / decoding, ciphering / deciphering, breaker, translator), or the "Pick's Theorem" functions (calculate, convert, solve, decrypt / encrypt, decipher / cipher, decode / encode, translate) written in any informatic language (Python, Java, PHP, C#, Javascript, Matlab, etc.) and all data download, script, or API access for "Pick's Theorem" are not public, same for offline use on PC, mobile, tablet, iPhone or Android app!
Reminder : dCode is free to use.
Cita dCode
The copy-paste of the page "Pick's Theorem" or any of its results, is allowed (even for commercial purposes) as long as you cite dCode!
Exporting results as a .csv or .txt file is free by clicking on the export icon
Cite as source (bibliography):
Pick's Theorem on dCode.fr [online website], retrieved on 2024-04-19,
